Dokumentations-Portal
- Anwenderhilfe
- Administrationsdokumentation
- Entwicklerdokumentation
Here you find help on the use of TeX in Stud.IP.
Some of you may have noticed that our computer keyboard does not have a sigma sign 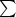 , an integral sign
, an integral sign 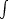 or similar symbols. Because we occasionally need them for university operations, Stud.IP implemented TeX-Arithmetic (pronounced Tech) in order to be able to insert mathematical symbols and entire formulae.
or similar symbols. Because we occasionally need them for university operations, Stud.IP implemented TeX-Arithmetic (pronounced Tech) in order to be able to insert mathematical symbols and entire formulae.
You generally write:
[tex] f(x) = e^{x+1} [/tex]
so this becomes, for example:
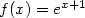
This means that the bracketed terms [tex] [/tex] form the frame for the formula. Normal TeX code, such as that used by other programmes and websites, can be placed inside the TeX brackets (or TeX tags). The TeX code has become a certain standard, but it will be briefly explained.
In principal one can write in TeX tags the same way as in other contexts. All formulae, which contain +, -, *, / and whole numbers and letters are written in TeX in the same manner in which one would have written them otherwise. In TeX the other symbols are merely designated by specific character sequences. The character sequence \sum thus results in a sigma sign.
Example:
[tex] \sum [/tex] becomes 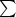
Similarly, the integral sign is signified by \int 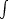 etc. A comprehensive list is presented below.
etc. A comprehensive list is presented below.
But, to begin with, here are a few syntax rules for TeX. For the sigma sign one wants to specifically state the variables across which the variables are summed (and how often) and for the integral sign the limits of the integration (or quantities). This is performed as follows:
[tex] \sum_1^9 [/tex]
becomes 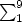
The _ (underline) always shows the term which should be at the bottom (subscript) (as in the customary Stud.IP syntax as well) and the ^ sign does the same for superscript characters. And this applies for the sigma sign, integral sign but — and now things are getting cool — also for normal variable indices or powers.
Example:
[tex] f(x) = x^7 [/tex] wird zu 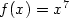
In other words this is a notation for everything. If the expressions which are to be subscripts or superscripts are more complicated than one character (and even the number 10 comprises more than one character) one has to write the entire expression in braces { and }, so that it will be considered to be a collective expression. In effect the expression in braces { and } has a character length of 1 for TeX. Now an example for such "complicated“ expressions:
Example:
[tex]\sum_1^100[/tex] becomes 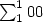 .
That is not what we usually desire, thus we have to write
.
That is not what we usually desire, thus we have to write
[tex]\sum_1^{100}[/tex], which becomes 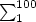 .
And now another real example:
.
And now another real example:
[tex]\sum_{k = 1}^n 1/k [/tex] becomes 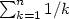
And now to fractions. In most cases a fraction is well written with the / (slash) character, such as 1/7 for example. But large fractions in particularly become confusing when written in this manner. In TeX fractions can be represented by writing the fraction line as \over. Everything in front of this is considered the numerator; everything behind it is interpreted as the denominator of the fraction.
Example:
[tex] x + 3 \over y + 2 [/tex] becomes 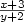
But this becomes problematical when something other than the fraction is to be written. In this case one writes the fraction in braces { and } and everything that is not contained in the braces is not part of the fraction.
Example:
false: [tex] f(x) = x + 3 \over 5 [/tex] becomes 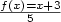
correct: [tex] f(x) = x + {3 \over 5} [/tex] becomes 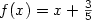
TeX can also depict compound fractions. To achieve this, one simply writes another fraction in braces in a fraction:
Example:
[tex]f_n(x) = \left {3 + x \over 1 + {1 \over n} } [/tex] becomes 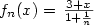
Unfortunately, the same thing applies in TeX as in real life: one should avoid double fractions. In real life they become confusing and in TeX the characters gradually become too small. At least, a certain minimum size is never exceeded in TeX so that one can use an infinite number of braces.
Example:
[tex]f_n(x) = \left {3 + x \over 1 + {1 \over 1 + {1 \over 1 + {1 \over 1 + {1 \over n}}}} } [/tex]
becomes
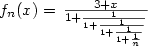
It is not pretty, but it works.
The fact that an orderly formula in TeX is rather complicated is beyond dispute. But let’s say it like this: it is more difficult to read TeX code than to write it. Basically, one only has to understand the TeX principle and formulae nearly write themselves.




There are a number of matrices, which all begin with \matrix. The type of matrix is then written in braces (i.e., the type of brackets which should enclose it). Then all cells are written individually from left to right and from top to bottom. An & symbol indicates that a cell should be indented and a // shows that a cell shifts downwards.


< Formatting text | Overview | Stud.IP rank list >